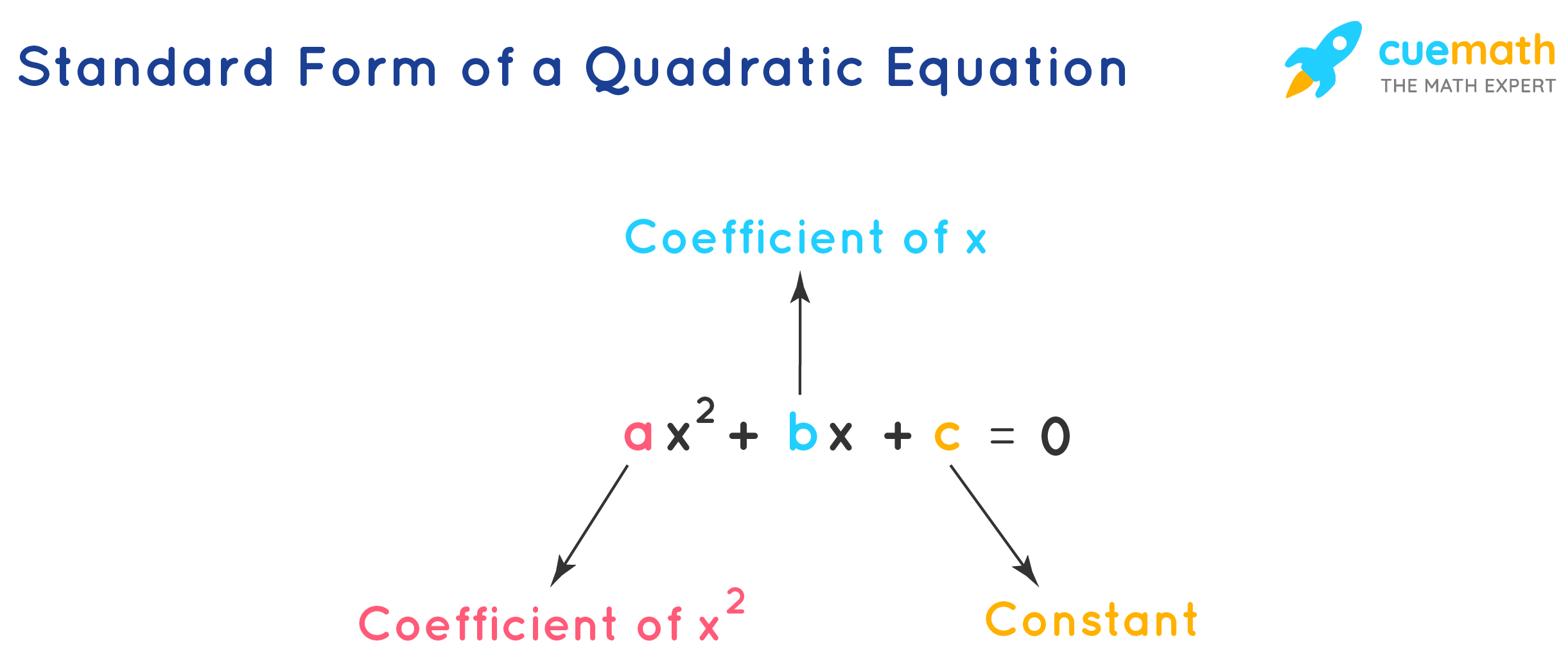
of quadratic equation is a x squared all plus b x plus c equals 0. Here, a, b, and c are constants." width="" />The standard form of quadratic equation is ax 2 + bx + c = 0, where 'a' is the leading coefficient and it is a non-zero real number. This equation is called 'quadratic' as its degree is 2 because 'quad' means 'square'. Apart from the standard form of quadratic equation, a quadratic equation can be written in other forms.
Let us learn more about the standard form of a quadratic equation and let us see how to convert one form of a quadratic equation into another.
| 1. | What is the Standard Form of Quadratic Equation? |
| 2. | Converting Standard Form of Quadratic Equation into Vertex Form |
| 3. | Converting Standard Form of Quadratic Equation into Intercept Form |
| 4. | FAQs on Standard Form of Quadratic Equation |
The standard form of quadratic equation with a variable x is of the form ax 2 + bx + c = 0, where a ≠ 0, and a, b, and c are real numbers. Here, b and c can be either zeros or non-zero numbers and
of quadratic equation is a x squared all plus b x plus c equals 0. Here, a, b, and c are constants." width="" />
Here are some examples of quadratic equations in standard form.
The standard form of a quadratic equation is also known as its general form. Thus, the general form of a quadratic equation is also of the form ax 2 + bx + c = 0, where a ≠ 0.
Let us convert the standard form of a quadratic equation ax 2 + bx + c = 0 into the vertex form a (x - h) 2 + k = 0 (where (h, k) is the vertex of the quadratic function f(x) = a (x - h) 2 + k). Note that the value of 'a' is the same in both equations. Let us just set them equal to know the relation between the variables.
ax 2 + bx + c = a (x - h) 2 + k
ax 2 + bx + c = a (x 2 - 2xh + h 2 ) + k
ax 2 + bx + c = ax 2 - 2ah x + (ah 2 + k)
Comparing the coefficients of x on both sides,
b = -2ah ⇒ h = -b/2a . (1)
Comparing the constants on both sides,
c = ah 2 + k
c = a (-b/2a) 2 + k (From (1))
c = b 2 /(4a) + k
k = c - (b 2 /4a)
k = (4ac - b 2 ) / (4a)
Thus, we can use the formulas h = -b/2a and k = (4ac - b 2 ) / (4a) to convert the standard to vertex form.
Consider the quadratic equation 2x 2 - 4x + 3 = 0. Comparing this with ax 2 + bx + c = 0, we get a = 2, b = -4, and c = 3. To convert it into the vertex form, let us find the values of h and k.
Substituting a = 2, h = 1, and k = 1 in the vertex form a (x - h) 2 + k = 0, we get:
The process of converting the vertex form of a quadratic equation into the standard form is pretty simple and it is done by simply evaluating (x - h) 2 = (x - h) (x - h) and simplifying. Let us consider the above example 2 (x - 1) 2 + 1 = 0 and let us convert it back into standard form.
2 (x - 1) 2 + 1 = 0 -------> Vertex Form
2 (x - 1) (x - 1) + 1 = 0
2 (x 2 - x - x + 1) + 1 = 0
2 (x 2 - 2x + 1) + 1 = 0
2x 2 - 4x + 2 + 1 = 0
2x 2 - 4x + 3 = 0 --------> Standard Form
Let us convert the standard form of a quadratic equation ax 2 + bx + c = 0 into the vertex form a (x - p)(x - q) = 0. Here, (p, 0) and (q, 0) are the x-intercepts of the quadratic function f(x) = ax 2 + bx + c) and hence p and q are the roots of the quadratic equation. Thus, we just use any one of the solving quadratic equation techniques to find p and q.
Consider the quadratic equation in standard form 2x 2 - 7x + 5 = 0. By comparing this with ax 2 + bx + c = 0, we get a = 2. Now we will solve the quadratic equation by factorization.
2x 2 - 7x + 5 = 0
2x 2 - 2x - 5x + 5 = 0
2x (x - 1) - 5 (x - 1) = 0
(x - 1) (2x - 5) = 0
x - 1 = 0; 2x - 5 =0
x = 1; x = 5/2
Thus, p = 1 and q = 5/2
Thus, the intercept form is,
a (x - p)(x - q) = 0
2 (x - 1) (x - 5/2) = 0
2 (x - 1) (2x - 5)/2 = 0
(x - 1) (2x - 5) = 0
The process of converting the intercept form of a quadratic equation into standard form is really easy and it is done by simply multiplying the binomials (x - p) (x - q) and simplifying. Let us consider the above example (x - 1) (2x - 5) = 0 and let us convert it back into standard form.
(x - 1) (2x - 5) = 0 -------> Intercept Form
2x 2 - 5x - 2x + 5 = 0
2x 2 - 7x + 5 = 0 --------> Standard Form
Important Notes on Standard Form of Quadratic Equation:
☛Related Topics:
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
Example 1: Which of the following quadratic equations are in the standard form? a) 2x 2 - 3x - 5 = 0 b) 0x 2 - 3x + 5 = 0 Solution: We know that the standard form of a quadratic equation is ax 2 + bx + c = 0, where 'a' is not equal to 0. Thus, in the given equations, only (a) is in the standard form ☛Note: Part b) has a = 0 and hence it becomes -3x + 5 = 0, which is a linear equation. Answer: a) 2x 2 - 3x - 5= 0 is in the standard form.
Example 2: Write the standard form of quadratic equation for the given expression: (x - 7) ( x - 8) = 0 Solution: Let us convert the given equation into the standard form of quadratic equation (ax 2 + bx + c = 0) (x - 7) ( x - 8) = 0
x 2 - 7x - 8x + 56 = 0
x 2 - 15x + 56 = 0 Answer: The standard form of the given quadratic equation is x 2 - 15x + 56 = 0.
Substituting all these values in the vertex form a(x - h) 2 + k = 0, we get:
3 (x - 3) 2 - 26 = 0
Answer: The given quadratic equation in vertex form is 3 (x - 3) 2 - 26 = 0.
View Answer >
Become a problem-solving champ using logic, not rules. Learn the why behind math with our certified experts
